2622. Надежные
сети
Вы отвечаете за
проектирование сети в кампусе между зданиями и очень беспокоитесь о ее
надежности и стоимости. Вы решили добавить некоторую избыточность в сети,
сохраняя при этом ее как можно дешевой. В частности, Вы хотите построить такую
самую дешевую сеть, что если какая-либо одна линия связи перестанет работать,
тем не менее связь между всеми зданиями все еще будет существовать. Такую сеть
будем называть минимальной надежной сетью.
Вход. Состоит из
нескольких тестов. Каждый тест начинается со строки, содержащей пару целых
чисел n (n ≤ 15) и m (m ≤ 20) – количество зданий
(пронумерованных от 1 до n) и
количество возможных соединений между зданиями. Каждая из следующих m строк имеет вид b1 b2
c (все числа натуральные),
указывающая на то, что стоимость соединения зданий b1 и b2
равна с. Все связи двунаправленные.
Последний тест
содержит n = m = 0 и не обрабатывается.
Выход. Для каждого
теста вывести одну строку, содержащую стоимость минимальной надежной сети. Если
такая сеть существует, то вывод должен иметь формат:
The minimal cost for
test case p is c.
где p номер теста (начиная с 1), а c
стоимость. Если надежной сети не существует, следует вывести следующую строку:
There is no reliable
net possible for test case p.
Пример входа
4 5
1 2 1
1 3 2
2 4 2
3 4 1
2 3 1
2 1
1 2 5
0 0
Пример выхода
The minimal cost for test
case 1 is 6.
There is no reliable net
possible for test case 2.
РЕШЕНИЕ
графы –
двусвязные компоненты
Анализ
алгоритма
Сеть является надежной, если граф, который ее представляет,
является реберно двусвязным. Двусвязность проверяется поиском в глубину – для
ее обеспечения необходимо отсутствие в графе мостов. Если входной граф не
является реберно двусвязным, то искомой сети не существует. При этом граф
допускает присутствие точек сочленения.
Используя динамическое программирование и маски, перебираем все
ребра и пробуем исключить их из входного графа. То есть перебираем все
возможные подграфы. Как только очередной подграф перестанет быть двусвязным
(будет содержать мост), перебор останавливаем. Среди всех двусвязных подграфов
ищем тот, который имеет наименьшую стоимость.
Пример
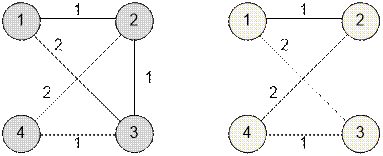
Рассмотрим первый граф, приведенный в примере. Минимальная
надежная сеть изображена справа. Граф справа
не содержит мостов, его стоимость равна 6.
Реализация
алгоритма
Входной граф храним в матрице смежности g. Массивы used, d и up
используются для проверки графа на двусвязность. Ячейка best[mask] хранит минимальную стоимость сети,
которую можно образовать из ребер, задаваемых маской mask.
#define INF 0x3F3F3F3F
#define MaxV 30
int g[MaxV][MaxV];
int
used[MaxV], d[MaxV], up[MaxV];
int
best[1<<20];
Список
ребер входного графа храним в явном виде в массиве структур E.
struct Edge
{
int u, v,
dist;
}
E[21];
Поиск в глубину dfs проверяет наличие мостов в графе.
Если мост присутствует, то переменная IsBridge
устанавливается равной 1.
void
dfs (int v, int
p = -1)
{
if (IsBridge)
return;
used[v] = 1;
d[v] = up[v] = time++;
for (int to = 1; to <= n; to++)
{
if ((to ==
p) || !g[v][to]) continue;
if
(used[to])
up[v] = min (up[v], d[to]);
else
{
dfs (to, v);
up[v] = min (up[v], up[to]);
if
(up[to] > d[v]) IsBridge = 1;
}
}
}
Функция IsBiconnected
возвращает 1, если граф реберно двусвязный. Для этого в графе должны
отсутствовать мосты.
int
IsBiconnected(void)
{
time = 1; IsBridge = 0;
memset(used,0,sizeof(used));
memset(d,0,sizeof(d));
memset(up,0,sizeof(used));
for(int i = 1; i <= n; i++)
{
if
(!used[i]) dfs(i);
if
(IsBridge) break;
}
return
!IsBridge;
}
Вычисляем минимальную стоимость сети, которую можно
образовать из ребер, задаваемых маской mask.
Длина всех ребер подграфа, задаваемого маской mask, равна CurLen.
int
go(int mask, int
CurLen)
{
int i, opt;
Если
значение best[mask] уже вычислено
(оно не равно INF), то возвращаем его. Если текущий подграф не является
двусвязным, то останавливаем процесс перебора, значение best[mask] полагаем равным INF – 1, что
считается уже вычисленным.
if(best[mask] != INF) return best[mask];
if (!IsBiconnected()) return best[mask] = INF - 1;
best[mask] = CurLen;
Перебираем
ребра, входящие в подграф. Удаляем из графа лишь одно i-ое ребро и рекурсивно решаем задачу для подграфа, который
задается маской mask XOR 2i. Длина ребер этого графа
будет равна CurLen – E[i].dist.
for(i = 0; i
< m; i++)
{
if (mask
& (1 << i))
{
g[E[i].u][E[i].v] = g[E[i].v][E[i].u] =
0;
opt = go(mask ^ (1 << i),CurLen -
E[i].dist);
if (opt
< best[mask]) best[mask] = opt;
g[E[i].u][E[i].v] = g[E[i].v][E[i].u] =
1;
}
}
return
best[mask];
}
Основная часть программы. Читаем
ребра графа и запоминаем их в массиве E. Строим матрицу смежности g. Дины
ребер хранятся только в массиве Е. Вычисляем длину всех ребер в переменной TotLen.
while(scanf("%d %d",&n,&m), n + m)
{
memset(best,0x3F,sizeof(best));
memset(g,0,sizeof(g));
res = INF;
TotLen = 0;
for(i = 0;
i < m; i++)
{
scanf("%d
%d %d",&E[i].u ,&E[i].v,&E[i].dist);
g[E[i].u][E[i].v] = g[E[i].v][E[i].u] =
E[i].dist;
TotLen += E[i].dist;
}
Находим
ответ и выводим его в зависимости от того, существует ли искомая надежная сеть.
Графу, который содержит все ребра, соответствует маска 2m – 1, состоящая из m
единиц.
res = go((1
<< m) - 1, TotLen);
if (res >= INF - 1)
printf("There is no reliable net possible for test case
%d.\n",cs++);
else printf("The
minimal cost for test case %d is %d.\n",cs++,res);
}